Note
Go to the end to download the full example code.
Reactors separated by a moving piston#
Two reactors separated by a piston that moves with a speed proportional to the pressure difference between the reactors.
Gas 1: a stoichiometric H2/O2/Ar mixture
Gas 2: a wet CO/O2 mixture
-------------------------------------
| || |
| || |
| gas 1 || gas 2 |
| || |
| || |
-------------------------------------
The two volumes are connected by an adiabatic free piston. The piston speed is proportional to the pressure difference between the two chambers.
Note that each side uses a different reaction mechanism
Requires: cantera >= 3.2.0, matplotlib >= 2.0
import cantera as ct
import matplotlib.pyplot as plt
plt.rcParams['figure.constrained_layout.use'] = True
Create objects representing the gases and reactors
gas1 = ct.Solution('h2o2.yaml')
gas1.TPX = 900.0, ct.one_atm, 'H2:2, O2:1, AR:20'
gas2 = ct.Solution('gri30.yaml')
gas2.TPX = 900.0, ct.one_atm, 'CO:2, H2O:0.01, O2:5'
r1 = ct.IdealGasReactor(gas1)
r1.volume = 0.5
r2 = ct.IdealGasReactor(gas2)
r2.volume = 0.1
The wall is held fixed until t = 0.1 s, then released to allow the pressure to equilibrate.
def v(t):
if t < 0.1:
return 0.0
else:
return (r1.phase.P - r2.phase.P) * 1e-4
w = ct.Wall(r1, r2, velocity=v)
net = ct.ReactorNet([r1, r2])
Run the simulation and collect the states of each reactor
states1 = ct.SolutionArray(r1.phase, extra=['t', 'volume'])
states2 = ct.SolutionArray(r2.phase, extra=['t', 'volume'])
fmt = '{:10.3f} {:10.1f} {:10.4f} {:10.4g} {:10.4g} {:10.4g} {:10.4g}'
print('{:>10} {:>10} {:>10} {:>10} {:>10} {:>10} {:>10}'.format(
'time [s]', 'T1 [K]', 'T2 [K]', 'V1 [m^3]', 'V2 [m^3]', 'Vtot [m^3]', 'X(CO)'))
for n in range(200):
time = (n+1)*0.001
net.advance(time)
if n % 4 == 3:
print(fmt.format(time, r1.T, r2.T, r1.volume, r2.volume,
r1.volume + r2.volume, r2.phase['CO'].X[0]))
states1.append(r1.phase.state, t=1000*time, volume=r1.volume)
states2.append(r2.phase.state, t=1000*time, volume=r2.volume)
time [s] T1 [K] T2 [K] V1 [m^3] V2 [m^3] Vtot [m^3] X(CO)
0.004 900.0 900.0015 0.5 0.1 0.6 0.2853
0.008 900.0 900.0030 0.5 0.1 0.6 0.2853
0.012 900.0 900.0046 0.5 0.1 0.6 0.2853
0.016 900.0 900.0062 0.5 0.1 0.6 0.2853
0.020 900.0 900.0078 0.5 0.1 0.6 0.2853
0.024 900.0 900.0094 0.5 0.1 0.6 0.2853
0.028 900.0 900.0111 0.5 0.1 0.6 0.2853
0.032 900.0 900.0128 0.5 0.1 0.6 0.2853
0.036 900.0 900.0146 0.5 0.1 0.6 0.2853
0.040 900.0 900.0163 0.5 0.1 0.6 0.2853
0.044 900.0 900.0181 0.5 0.1 0.6 0.2853
0.048 900.0 900.0199 0.5 0.1 0.6 0.2853
0.052 900.0 900.0218 0.5 0.1 0.6 0.2853
0.056 900.1 900.0237 0.5 0.1 0.6 0.2853
0.060 900.1 900.0256 0.5 0.1 0.6 0.2853
0.064 900.2 900.0276 0.5 0.1 0.6 0.2853
0.068 900.4 900.0296 0.5 0.1 0.6 0.2853
0.072 2205.8 900.0316 0.5 0.1 0.6 0.2853
0.076 2302.0 900.0336 0.5 0.1 0.6 0.2853
0.080 2303.0 900.0357 0.5 0.1 0.6 0.2853
0.084 2303.0 900.0378 0.5 0.1 0.6 0.2853
0.088 2303.0 900.0399 0.5 0.1 0.6 0.2853
0.092 2303.0 900.0421 0.5 0.1 0.6 0.2853
0.096 2303.0 900.0443 0.5 0.1 0.6 0.2853
0.100 2303.0 900.0466 0.5 0.1 0.6 0.2853
0.104 2231.1 1038.9822 0.5361 0.06393 0.6 0.2853
0.108 2220.8 1080.2525 0.5434 0.05656 0.6 0.2853
0.112 2220.4 1086.6947 0.5443 0.05572 0.6 0.2852
0.116 2220.7 1090.4472 0.5443 0.05571 0.6 0.2849
0.120 2221.1 1098.0337 0.5441 0.05591 0.6 0.2841
0.124 2222.0 1114.8905 0.5436 0.05639 0.6 0.2825
0.128 2224.5 1168.1365 0.5424 0.05764 0.6 0.2774
0.132 2296.5 2821.8695 0.5066 0.09336 0.6 0.03461
0.136 2313.6 2784.9365 0.4953 0.1047 0.6 0.03187
0.140 2317.9 2776.9144 0.4926 0.1074 0.6 0.03128
0.144 2319.0 2774.9214 0.492 0.108 0.6 0.03114
0.148 2319.3 2774.4116 0.4918 0.1082 0.6 0.0311
0.152 2319.3 2774.2803 0.4917 0.1083 0.6 0.03109
0.156 2319.4 2774.2464 0.4917 0.1083 0.6 0.03109
0.160 2319.4 2774.2376 0.4917 0.1083 0.6 0.03109
0.164 2319.4 2774.2354 0.4917 0.1083 0.6 0.03109
0.168 2319.4 2774.2348 0.4917 0.1083 0.6 0.03109
0.172 2319.4 2774.2347 0.4917 0.1083 0.6 0.03109
0.176 2319.4 2774.2346 0.4917 0.1083 0.6 0.03109
0.180 2319.4 2774.2346 0.4917 0.1083 0.6 0.03109
0.184 2319.4 2774.2346 0.4917 0.1083 0.6 0.03109
0.188 2319.4 2774.2346 0.4917 0.1083 0.6 0.03109
0.192 2319.4 2774.2346 0.4917 0.1083 0.6 0.03109
0.196 2319.4 2774.2346 0.4917 0.1083 0.6 0.03109
0.200 2319.4 2774.2346 0.4917 0.1083 0.6 0.03109
Plot the results
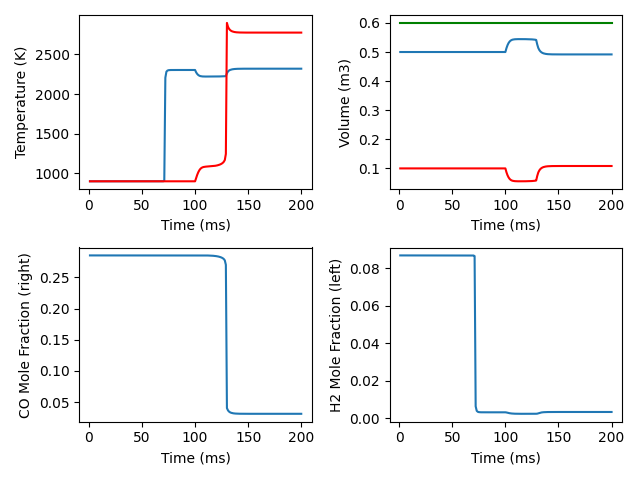
fig, ax = plt.subplots(2, 2)
ax[0,0].plot(states1.t, states1.T, '-', states2.t, states2.T, 'r-')
ax[0,0].set(xlabel='Time (ms)', ylabel='Temperature (K)')
ax[0,1].plot(states1.t, states1.volume, '-', states2.t, states2.volume, 'r-',
states1.t, states1.volume + states2.volume, 'g-')
ax[0,1].set(xlabel='Time (ms)', ylabel='Volume (m3)')
ax[1,0].plot(states2.t, states2('CO').X)
ax[1,0].set(xlabel='Time (ms)', ylabel='CO Mole Fraction (right)')
ax[1,1].plot(states1.t, states1('H2').X)
ax[1,1].set(xlabel='Time (ms)', ylabel='H2 Mole Fraction (left)')
plt.show()
Total running time of the script: (0 minutes 0.770 seconds)

