Note

Go to the end to download the full example code.

Solid oxide fuel cell using elementary kinetics#

A simple model of a solid oxide fuel cell.

Unlike most SOFC models, this model does not use semi-empirical Butler-Volmer kinetics for the charge transfer reactions, but uses elementary, reversible reactions obeying mass-action kinetics for all reactions, including charge transfer. As this script will demonstrate, this approach allows computing the OCV (it does not need to be separately specified), as well as polarization curves.

Caution

The parameters here, and in the input file sofc.yaml, are not to be relied upon for a real SOFC simulation! They are meant to illustrate only how to do such a calculation in Cantera. While some of the parameters may be close to real values, others are simply set arbitrarily to give reasonable-looking results.

It is recommended that you read input file sofc.yaml before reading or running this script.

Requires: cantera >= 2.6.0, scipy, pandas

Tags: Python kinetics electrochemistry surface chemistry fuel cell

import cantera as ct
import math
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.optimize import newton

ct.add_module_directory()

# parameters
T = 1073.15  # T in K
P = ct.one_atm  # One atm in Pa

# gas compositions. Change as desired.
anode_gas_X = 'H2:0.97, H2O:0.03'
cathode_gas_X = 'O2:1.0, H2O:0.001'

# time to integrate coverage eqs. to steady state in
# 'advance_coverages'. This should be more than enough time.
tss = 50.0

sigma = 2.0  # electrolyte conductivity [Siemens / m]
ethick = 5.0e-5  # electrolyte thickness [m]
TPB_length_per_area = 1.0e7  # TPB length per unit area [1/m]


def show_coverages(s):
    """Print the coverages for surface s."""
    print('\n{0}\n'.format(s.name))
    cov = s.coverages
    names = s.species_names
    for n in range(s.n_species):
        print('{0:16s}  {1:13.4g}'.format(names[n], cov[n]))


def equil_OCV(gas1, gas2):
    return (-ct.gas_constant * gas1.T *
            math.log(gas1['O2'].X[0] / gas2['O2'].X[0]) / (4.0 * ct.faraday))

Anode-side phases#

# import the anode-side triple phase boundary and adjacent phases
tpb_a = ct.Interface("sofc.yaml", "tpb")
anode_surf = tpb_a.adjacent["metal_surface"]
oxide_surf_a = tpb_a.adjacent["oxide_surface"]
anode_bulk = tpb_a.adjacent["metal"]
oxide_a = oxide_surf_a.adjacent["oxide_bulk"]
gas_a = oxide_surf_a.adjacent["gas"]

anode_surf.name = 'anode surface'
oxide_surf_a.name = 'anode-side oxide surface'

# this function is defined to use with a Newton solver to invert the current-
# voltage function. The Newton solver requires a function of one variable, so the
# other objects are accessed through the global namespace.
def anode_curr(E):
    """
    Current from the anode as a function of anode potential relative to
    electrolyte.
    """

    # the anode-side electrolyte potential is kept at zero. Therefore, the
    # anode potential is just equal to E.
    anode_bulk.electric_potential = E

    # get the species net production rates due to the anode-side TPB reaction
    # mechanism. The production rate array has the values for the neighbor
    # species in the order listed in the .yaml file, followed by the tpb phase.
    # The kinetics_species_index method finds the index of the species,
    # accounting for the possibility of species being in different orders in the
    # arrays.
    w = tpb_a.net_production_rates
    electron_index = tpb_a.kinetics_species_index('electron')

    # the sign convention is that the current is positive when
    # electrons are being delivered to the anode - that is, it is positive
    # for fuel cell operation.
    return ct.faraday * w[electron_index] * TPB_length_per_area

Cathode-side phases#

Here for simplicity we are using the same phase and interface models for the cathode as we used for the anode. In a more realistic simulation, separate models would be used for the cathode, with a different reaction mechanism.

# import the cathode-side triple phase boundary and adjacent phases
tpb_c = ct.Interface("sofc.yaml", "tpb")
cathode_surf = tpb_c.adjacent["metal_surface"]
oxide_surf_c = tpb_c.adjacent["oxide_surface"]
cathode_bulk = tpb_c.adjacent["metal"]
oxide_c = oxide_surf_c.adjacent["oxide_bulk"]
gas_c = oxide_surf_c.adjacent["gas"]

cathode_surf.name = 'cathode surface'
oxide_surf_c.name = 'cathode-side oxide surface'


def cathode_curr(E):
    """
    Current to the cathode as a function of cathode
    potential relative to electrolyte
    """

    # due to ohmic losses, the cathode-side electrolyte potential is non-zero.
    # Therefore, we need to add this potential to E to get the cathode
    # potential.
    cathode_bulk.electric_potential = E + oxide_c.electric_potential

    # get the species net production rates due to the cathode-side TPB
    # reaction mechanism. The production rate array has the values for the
    # neighbor species in the order listed in the .yaml file, followed by the
    # tpb phase. The kinetics_species_index method finds the index of the species,
    # accounting for the possibility of species being in different orders in the
    # arrays.
    w = tpb_c.net_production_rates
    electron_index = tpb_c.kinetics_species_index('electron')

    # the sign convention is that the current is positive when electrons are
    # being drawn from the cathode (that is, negative production rate).
    return -ct.faraday * w[electron_index] * TPB_length_per_area

Initialization#

set the gas compositions, and temperatures of all phases

gas_a.TPX = T, P, anode_gas_X
gas_a.equilibrate('TP')  # needed to use equil_OCV

gas_c.TPX = T, P, cathode_gas_X
gas_c.equilibrate('TP')  # needed to use equil_OCV

phases = [anode_bulk, anode_surf, oxide_surf_a, oxide_a, cathode_bulk,
          cathode_surf, oxide_surf_c, oxide_c, tpb_a, tpb_c]
for p in phases:
    p.TP = T, P

now bring the surface coverages into steady state with these gas compositions. Note that the coverages are held fixed at these values - we do NOT consider the change in coverages due to TPB reactions. For that, a more complex model is required. But as long as the thermal chemistry is fast relative to charge transfer, this should be an OK approximation.

for s in [anode_surf, oxide_surf_a, cathode_surf, oxide_surf_c]:
    s.advance_coverages(tss)
    show_coverages(s)

anode surface

(m)                      0.6187
H(m)                     0.3811
O(m)                   8.63e-05
OH(m)                 2.593e-06
H2O(m)                5.057e-05

anode-side oxide surface

(ox)                    0.04994
O''(ox)                  0.9489
OH'(ox)                0.001128
H2O(ox)               3.359e-08

cathode surface

(m)                   1.482e-07
H(m)                  7.572e-14
O(m)                          1
OH(m)                 2.492e-08
H2O(m)                4.033e-13

cathode-side oxide surface

(ox)                    0.04999
O''(ox)                  0.9498
OH'(ox)               0.0002061
H2O(ox)                1.12e-09

Find open circuit potentials by solving for the E values that give zero current.

Ea0 = newton(anode_curr, x0=-0.51)
Ec0 = newton(cathode_curr, x0=0.51)

print('\nocv from zero current is: ', Ec0 - Ea0)
print('OCV from thermo equil is: ', equil_OCV(gas_a, gas_c))

print('Ea0 = ', Ea0)
print('Ec0 = ', Ec0)

ocv from zero current is:  1.137576853535033
OCV from thermo equil is:  1.1375768535347215
Ea0 =  -0.7334421804359453
Ec0 =  0.4041346730990877

Polarization curve#

Vary the anode overpotentials from -250 mV (cathodic) to +250 mV (anodic)

Ea_min = Ea0 - 0.25
Ea_max = Ea0 + 0.25
Ec = 1.0  # initial guess for Newton solver

output_data = []

for Ea in np.linspace(Ea_min, Ea_max, 100):
    # set the electrode potential. Note that the anode-side electrolyte is
    # held fixed at 0 V.
    anode_bulk.electric_potential = Ea

    # compute the anode current
    curr = anode_curr(Ea)

    # set potential of the oxide on the cathode side to reflect the ohmic drop
    # through the electrolyte
    delta_V = curr * ethick / sigma

    # if the current is positive, negatively-charged ions are flowing from the
    # cathode to the anode. Therefore, the cathode side must be more negative
    # than the anode side.
    phi_oxide_c = -delta_V

    # note that both the bulk and the surface potentials must be set
    oxide_c.electric_potential = phi_oxide_c
    oxide_surf_c.electric_potential = phi_oxide_c

    # Find the value of the cathode potential relative to the cathode-side
    # electrolyte that yields the same current density as the anode current
    # density
    Ec = newton(lambda E: cathode_curr(E) - curr, x0=Ec)

    cathode_bulk.electric_potential = phi_oxide_c + Ec

    # write the current density, anode and cathode overpotentials, ohmic
    # overpotential, and load potential
    output_data.append([0.1*curr, Ea - Ea0, Ec - Ec0, delta_V,
                        cathode_bulk.electric_potential -
                        anode_bulk.electric_potential])

Collect data and save as CSV#

df = pd.DataFrame.from_records(
    output_data,
    index='i (mA/cm2)',
    columns=['i (mA/cm2)', 'eta_a', 'eta_c', 'eta_ohmic', 'Eload']
)
df.to_csv("sofc.csv")
print('polarization curve data written to file sofc.csv')

polarization curve data written to file sofc.csv

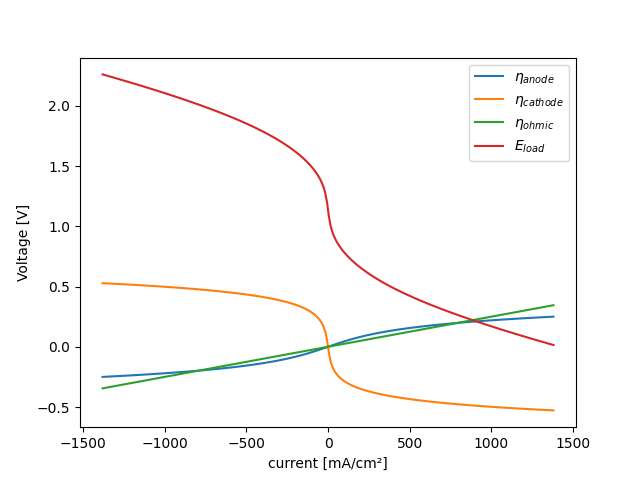
Plot results#

fig, ax = plt.subplots()
ax.plot(df.index, df.eta_a, label=r'$\eta_{anode}$')
ax.plot(df.index, df.eta_c, label=r'$\eta_{cathode}$')
ax.plot(df.index, df.eta_ohmic, label=r'$\eta_{ohmic}$')
ax.plot(df.index, df.Eload, label=r'$E_{load}$')
ax.set(xlabel='current [mA/cm²]', ylabel='Voltage [V]')
ax.legend()
sofc

Total running time of the script: (0 minutes 0.305 seconds)

Gallery generated by Sphinx-Gallery