Note
Go to the end to download the full example code.
Combustor residence time#
Calculate steady-state solutions for a combustor, modeled as a single well-stirred reactor, for different residence times.
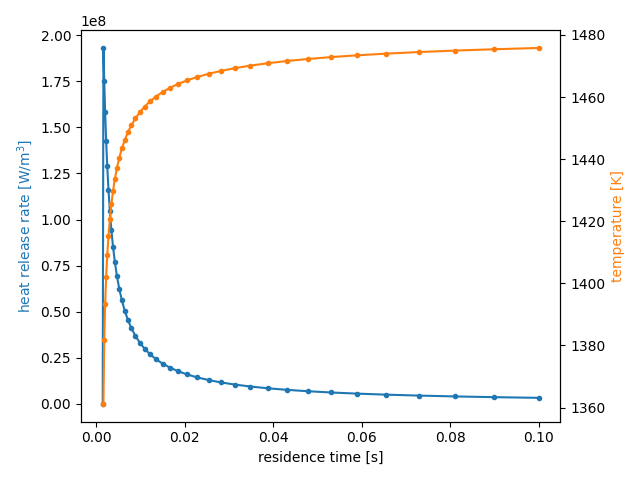
We are interested in the steady-state burning solution. This example explores the effect of changing the residence time on completeness of reaction (through the burned gas temperature) and on the total heat release rate.
Demonstrates the use of a MassFlowController where the mass flow rate function
depends on variables other than time by capturing these variables from the
enclosing scope. Also shows the use of a PressureController to create a constant
pressure reactor with a fixed volume.
Requires: cantera >= 3.0, matplotlib >= 2.0
import numpy as np
import matplotlib.pyplot as plt
import cantera as ct
Use reaction mechanism GRI-Mech 3.0. For 0-D simulations, no transport model is necessary.
gas = ct.Solution('gri30.yaml', transport_model=None)
Create a Reservoir for the inlet, set to a methane/air mixture at a specified
equivalence ratio
equiv_ratio = 0.5 # lean combustion
gas.TP = 300.0, ct.one_atm
gas.set_equivalence_ratio(equiv_ratio, 'CH4:1.0', 'O2:1.0, N2:3.76')
inlet = ct.Reservoir(gas)
Create the combustor, and fill it initially with a mixture consisting of the equilibrium products of the inlet mixture. This state corresponds to the state the reactor would reach with infinite residence time, and thus provides a good initial condition from which to reach a steady-state solution on the reacting branch.
gas.equilibrate('HP')
combustor = ct.IdealGasReactor(gas)
combustor.volume = 1.0
Create a reservoir for the exhaust:
Use a variable mass flow rate to keep the residence time in the reactor
constant (residence_time = mass / mass_flow_rate). The mass flow rate function
can access variables defined in the calling scope, including state variables
of the Reactor object (combustor) itself.
def mdot(t):
return combustor.mass / residence_time
inlet_mfc = ct.MassFlowController(inlet, combustor, mdot=mdot)
A PressureController has a baseline mass flow rate matching the primary
MassFlowController, with an additional pressure-dependent term. By explicitly
including the upstream mass flow rate, the pressure is kept constant without
needing to use a large value for K, which can introduce undesired stiffness.
outlet_mfc = ct.PressureController(combustor, exhaust, primary=inlet_mfc, K=0.01)
Run a loop over decreasing residence times, until the reactor is extinguished, saving the state after each iteration.
# the simulation only contains one reactor
sim = ct.ReactorNet([combustor])
states = ct.SolutionArray(gas, extra=['tres'])
residence_time = 0.1 # starting residence time
while combustor.T > 500:
sim.initial_time = 0.0 # reset the integrator
sim.advance_to_steady_state()
print('tres = {:.2e}; T = {:.1f}'.format(residence_time, combustor.T))
states.append(combustor.thermo.state, tres=residence_time)
residence_time *= 0.9 # decrease the residence time for the next iteration
tres = 1.00e-01; T = 1475.8
tres = 9.00e-02; T = 1475.4
tres = 8.10e-02; T = 1474.9
tres = 7.29e-02; T = 1474.5
tres = 6.56e-02; T = 1474.0
tres = 5.90e-02; T = 1473.4
tres = 5.31e-02; T = 1472.9
tres = 4.78e-02; T = 1472.2
tres = 4.30e-02; T = 1471.6
tres = 3.87e-02; T = 1470.9
tres = 3.49e-02; T = 1470.1
tres = 3.14e-02; T = 1469.3
tres = 2.82e-02; T = 1468.4
tres = 2.54e-02; T = 1467.5
tres = 2.29e-02; T = 1466.5
tres = 2.06e-02; T = 1465.4
tres = 1.85e-02; T = 1464.2
tres = 1.67e-02; T = 1463.0
tres = 1.50e-02; T = 1461.6
tres = 1.35e-02; T = 1460.2
tres = 1.22e-02; T = 1458.6
tres = 1.09e-02; T = 1456.9
tres = 9.85e-03; T = 1455.1
tres = 8.86e-03; T = 1453.1
tres = 7.98e-03; T = 1451.0
tres = 7.18e-03; T = 1448.7
tres = 6.46e-03; T = 1446.2
tres = 5.81e-03; T = 1443.4
tres = 5.23e-03; T = 1440.5
tres = 4.71e-03; T = 1437.2
tres = 4.24e-03; T = 1433.7
tres = 3.82e-03; T = 1429.8
tres = 3.43e-03; T = 1425.5
tres = 3.09e-03; T = 1420.7
tres = 2.78e-03; T = 1415.3
tres = 2.50e-03; T = 1409.1
tres = 2.25e-03; T = 1401.9
tres = 2.03e-03; T = 1393.2
tres = 1.82e-03; T = 1381.8
tres = 1.64e-03; T = 1361.2
tres = 1.48e-03; T = 300.0
Plot results:
f, ax1 = plt.subplots(1, 1)
ax1.plot(states.tres, states.heat_release_rate, '.-', color='C0')
ax2 = ax1.twinx()
ax2.plot(states.tres[:-1], states.T[:-1], '.-', color='C1')
ax1.set_xlabel('residence time [s]')
ax1.set_ylabel('heat release rate [W/m$^3$]', color='C0')
ax2.set_ylabel('temperature [K]', color='C1')
f.tight_layout()
plt.show()
Total running time of the script: (0 minutes 0.831 seconds)

