Note
Go to the end to download the full example code.
Diffusion flame unstable branch#
This example uses the two-point flame control feature to march solutions down the stable and unstable burning branch for a counterflow diffusion flame. A hydrogen-oxygen diffusion flame at 1 bar is studied.
Requires: cantera >= 3.1, matplotlib >= 2.0
import logging
import sys
from pathlib import Path
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import cantera as ct
logger = logging.getLogger(__name__)
logger.setLevel(logging.INFO)
logging.basicConfig(stream=sys.stdout)
Flame Initialization#
# Set up an initial hydrogen-oxygen counterflow flame at 1 bar and low strain
# rate (maximum axial velocity gradient = 2414 1/s)
reaction_mechanism = 'h2o2.yaml'
gas = ct.Solution(reaction_mechanism)
width = 18.e-3 # 18mm wide
f = ct.CounterflowDiffusionFlame(gas, width=width)
# Define the operating pressure and boundary conditions
f.P = 1.0e5 # 1 bar
f.fuel_inlet.mdot = 0.5 # kg/m^2/s
f.fuel_inlet.X = 'H2:1'
f.fuel_inlet.T = 300 # K
f.oxidizer_inlet.mdot = 3.0 # kg/m^2/s
f.oxidizer_inlet.X = 'O2:1'
f.oxidizer_inlet.T = 500 # K
# Set refinement parameters
f.set_refine_criteria(ratio=4.0, slope=0.1, curve=0.2, prune=0.05)
# Initialize and solve
logger.info('Creating the initial solution')
f.solve(loglevel=0, auto=True)
# Define output locations
output_path = Path() / "diffusion_flame_continuation_data"
output_path.mkdir(parents=True, exist_ok=True)
INFO:__main__:Creating the initial solution
Flame Continuation#
# Maximum number of steps to take
n_max = 1000
# Relative temperature defining control point locations, with 1 being the peak
# temperature and 0 being the inlet temperature. Lower values tend to avoid solver
# failures early on, while using higher values on the unstable branch tend to help
# with finding solutions where the peak temperature is very low.
initial_spacing = 0.6
unstable_spacing = 0.95
# Amount to adjust temperature at the control point each step [K]
temperature_increment = 20.0
max_increment = 100
# Try to keep T_max from changing more than this much each step [K]
target_delta_T_max = 20
# Stop after this many successive errors
max_error_count = 3
error_count = 0
# Stop after any failure if the strain rate has dropped to this fraction of the maximum
strain_rate_tol = 0.10
f.two_point_control_enabled = True
# Prevent two point control from finding solutions with negative inlet velocities
f.flame.set_bounds(spread_rate=(-1e-5, 1e20))
f.max_time_step_count = 100
T_max = max(f.T)
a_max = strain_rate = f.strain_rate('max')
data = [] # integral output quantities for each step
logger.info('Starting two-point control')
for i in range(n_max):
if strain_rate > 0.98 * a_max:
spacing = initial_spacing
else:
spacing = unstable_spacing
control_temperature = np.min(f.T) + spacing*(np.max(f.T) - np.min(f.T))
# Store the flame state in case the iteration fails and we need to roll back
backup_state = f.to_array()
logger.debug(f'Iteration {i}: Control temperature = {control_temperature:.2f} K')
f.set_left_control_point(control_temperature)
f.set_right_control_point(control_temperature)
# This decrement is what drives the two-point control. If failure
# occurs, try decreasing the decrement.
f.left_control_point_temperature -= temperature_increment
f.right_control_point_temperature -= temperature_increment
f.clear_stats()
if (f.left_control_point_temperature < f.fuel_inlet.T + 100
or f.right_control_point_temperature < f.oxidizer_inlet.T + 100
):
logger.info("SUCCESS! Stopping because control point temperature is "
"sufficiently close to inlet temperature.")
break
try:
f.solve(loglevel=0)
if abs(max(f.T) - T_max) < 0.8 * target_delta_T_max:
# Max temperature is changing slowly. Try a larger increment next step
temperature_increment = min(temperature_increment + 3, max_increment)
elif abs(max(f.T) - T_max) > target_delta_T_max:
# Max temperature is changing quickly. Scale down increment for next step
temperature_increment *= 0.9 * target_delta_T_max / (abs(max(f.T) - T_max))
error_count = 0
except ct.CanteraError as err:
logger.debug(err)
if strain_rate / a_max < strain_rate_tol:
logger.info('SUCCESS! Traversed unstable branch down to '
f'{100 * strain_rate / a_max:.2f}% of the maximum strain rate.')
break
# Restore the previous solution and try a smaller temperature increment for the
# next iteration
f.from_array(backup_state)
temperature_increment = 0.7 * temperature_increment
error_count += 1
logger.warning(f"Solver did not converge on iteration {i}. Trying again with "
f"dT = {temperature_increment:.2f}")
if ct.hdf_support():
f.save(output_path / 'flame_profiles.h5', name=f'iteration{i}', overwrite=True)
# Collect output stats
T_max = max(f.T)
T_mid = 0.5 * (min(f.T) + max(f.T))
s = np.where(f.T > T_mid)[0][[0,-1]]
width = f.grid[s[1]] - f.grid[s[0]]
strain_rate = f.strain_rate('max')
a_max = max(strain_rate, a_max)
data.append({
'T_max': max(f.T),
'strain_rate': strain_rate,
'heat_release_rate': np.trapz(f.heat_release_rate, f.grid),
'n_points': len(f.grid),
'flame_width': width,
'Tc_increment': temperature_increment,
'time_steps': sum(f.time_step_stats),
'eval_count': sum(f.eval_count_stats),
'cpu_time': sum(f.jacobian_time_stats + f.eval_time_stats),
'errors': error_count
})
if error_count >= max_error_count:
logger.warning(f'FAILURE! Stopping after {error_count} successive solver '
'errors.')
break
logger.info(f'Stopped after {i} iterations')
INFO:__main__:Starting two-point control
/home/runner/work/cantera/cantera/build/doc/samples/python/onedim/diffusion_flame_continuation.py:165: DeprecationWarning: `trapz` is deprecated. Use `trapezoid` instead, or one of the numerical integration functions in `scipy.integrate`.
'heat_release_rate': np.trapz(f.heat_release_rate, f.grid),
INFO:__main__:SUCCESS! Traversed unstable branch down to 4.13% of the maximum strain rate.
INFO:__main__:Stopped after 134 iterations
Combine data#
df = pd.DataFrame.from_records(data)
df.to_csv(output_path / f'integral_data.csv')
df
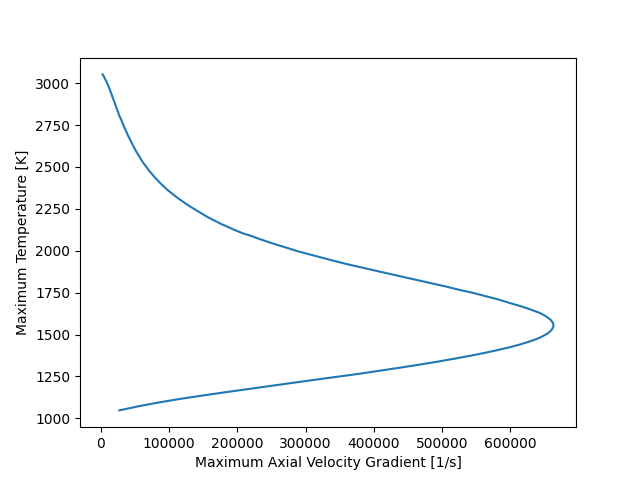
Plot the maximum temperature versus the maximum axial velocity gradient#
plt.figure()
plt.plot(df.strain_rate, df.T_max)
plt.xlabel('Maximum Axial Velocity Gradient [1/s]')
plt.ylabel('Maximum Temperature [K]')
plt.savefig(output_path / "figure_max_temperature_vs_max_velocity_gradient.png")
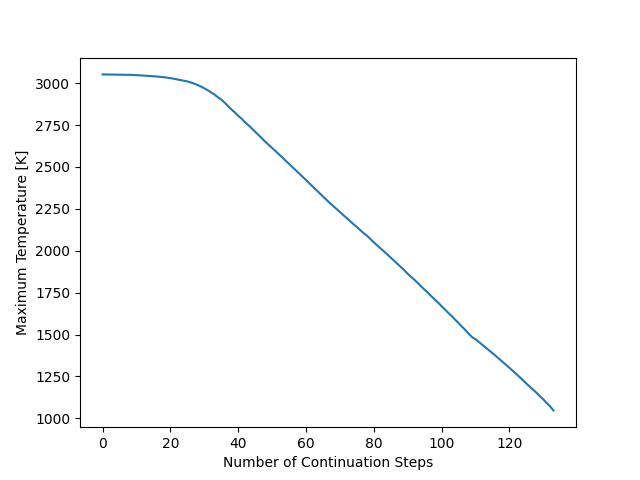
Plot maximum_temperature against number of iterations#
plt.figure()
plt.plot(df.T_max)
plt.xlabel('Number of Continuation Steps')
plt.ylabel('Maximum Temperature [K]')
plt.savefig(output_path / "figure_max_temperature_iterations.png")
plt.show()
Total running time of the script: (0 minutes 13.424 seconds)

