Plasma Reactor

Solve a constant pressure and constant gas/electron temperature plasma problem, which approximates the conditions found in a glow discharge.

This file uses a similar approach as custom.py, where the governing equations are implemented in Python, to solve the electron concentration in a plasma.

See the input file oxygen-plasma-itikawa.yaml.

Requires: cantera >= 3.1, matplotlib >= 2.0

Tags: Python combustion reactor network plasma

import cantera as ct
import numpy as np
import scipy.integrate

class ReactorOde:
    def __init__(self, plasma):
        # Parameters of the ODE system and auxiliary data are stored in the
        # ReactorOde object.
        self.gas = plasma
        self.P = plasma.P
        self.T = plasma.T

    def __call__(self, t, y):
        """the ODE function, y' = f(t,y) """

        # State vector is [Y_1, Y_2, ... Y_K]
        self.gas.set_unnormalized_mass_fractions(y)
        self.gas.TP = self.T, self.P
        rho = self.gas.density

        wdot = self.gas.net_production_rates
        dYdt = wdot * self.gas.molecular_weights / rho

        return np.hstack(dYdt)


plasma = ct.Solution('example_data/oxygen-plasma-itikawa.yaml',
                     'isotropic-electron-energy-plasma',
                      transport_model=None)

P = ct.one_atm * 0.01
T = 300.0
plasma.TPX = T, P, 'O2:1.0, e:5e-3, O2+:5e-3'
plasma.mean_electron_energy = 10 # [eV]
y0 = np.hstack(plasma.Y)

# Set up objects representing the ODE and the solver
ode = ReactorOde(plasma)
solver = scipy.integrate.ode(ode)
solver.set_integrator('vode', method='bdf', with_jacobian=True)
solver.set_initial_value(y0, 0.0)

# Integrate the equations, keeping T(t) and Y(k,t)
t_end = 1e-6
states = ct.SolutionArray(plasma, 1, extra={'t': [0.0]})
dt = 1e-9
while solver.successful() and solver.t < t_end:
    solver.integrate(solver.t + dt)
    plasma.TPY = T, P, solver.y
    states.append(plasma.state, t=solver.t)

# Plot the results
import matplotlib.pyplot as plt
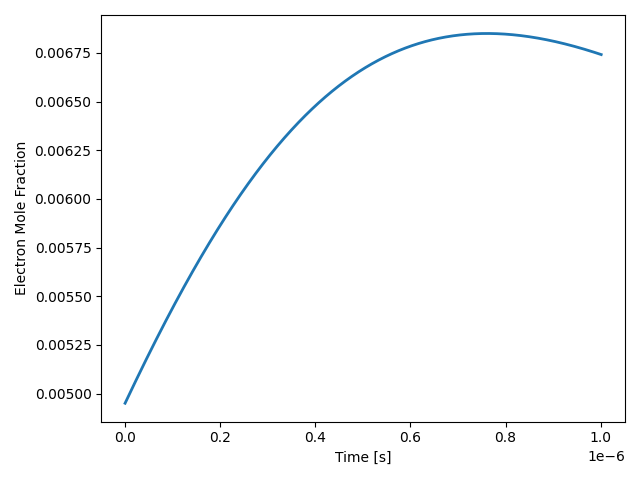
plt.plot(states.t, states('e').X, label='e', lw=2)
plt.ylabel('Electron Mole Fraction')
plt.xlabel('Time [s]')
plt.tight_layout()
plt.savefig("plasma-density")