Warning
This documentation is for an old version of Cantera. You can find docs for newer versions here.
Phases and their Interfaces¶
Now that we have covered how to write syntactically-correct input files, we can turn our attention to the content of the file. We’ll start by describing the entries for phases of various types, and the look at how to define interfaces between phases.
Phases¶
For each phase that appears in a problem, a corresponding entry should be present in the input file(s). For example, suppose we want to conduct a simulation with detailed chemistry of an idealized solid-oxide fuel cell shown below. The problem involves three solid phases (A nickel anode, a platinum cathode, and an oxygen-conducting yttrium-stabilized zirconia electrolyte), and two different gas phases (a fuel mixture on the anode side, and air on the cathode side). The problem also involves a number of interfaces at which heterogeneous chemistry may occur—two gas-metal interfaces, two gas-electrolyte interfaces, and two metal-electrolyte interfaces.
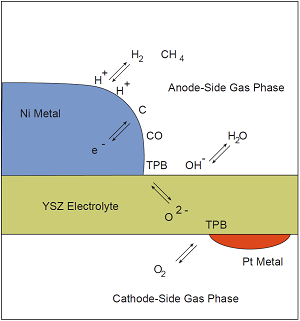
Phases entering into a hypothetical microkinetic simulation of an idealized solid-oxide fuel cell.
How to carry out this fuel cell simulation is beyond the scope of this document; we introduce it here only to give an example of the types of phases and interfaces that might need to be defined in order to carry out a simulation. (Of course, many simulations with Cantera only require defining a single phase.)
There are several different types of entries, corresponding to different types of phases. Phases are created using one of the directives corresponding to an implemented phase type:
ideal_gasstoichiometric_solidstoichiometric_liquidmetalsemiconductorincompressible_solidlatticelattice_solidliquid_vaporredlich_kwongideal_interfaceedge
These phase typese share many common features, however, and so we will begin by
discussing those aspects common to all entries for phases. The phase
class contains the features common to all phase types.
Phase Attributes¶
Phase Name¶
The name field is a string that identifies the phase. It must not contain
any whitespace characters or reserved XML characters, and must be unique within
the file among all phase definitions of any type.
Phases are referenced by name when importing them into an application program, or when defining an interface between phases.
Declaring the Elements¶
The elements that may be present in the phase are declared in the elements
field. This must be a string of element symbols separated by spaces. Each symbol
must either match one listed in the database file elements.xml, or else
match the symbol of an element entry defined elsewhere in the input file (See
Elements).
The elements.xml database contains most elements of the periodic table, with
their natural-abundance atomic masses. It also contains a few isotopes (D, Tr),
and an “element” for an electron (E). This pseudo-element can be used to specify
the composition of charged species. Note that two-character symbols should have
an uppercase first letter, and a lowercase second letter (e.g. Cu, not CU).
It should be noted that the order of the element symbols in the string determines the order in which they are stored internally by Cantera. For example, if a phase definition specifies the elements as:
ideal_gas(name = "gasmix",
elements = "H C O N Ar",
# ...
)
then when this definition is imported by an application, element-specific properties will be ordered in the same way:
>>> import cantera as ct
>>> gas = ct.Solution('example.cti', 'gasmix')
>>> for n in range(gas.nElements()):
... print n, gas.elementSymbol(n)
0 H
1 C
2 O
3 N
4 Ar
For some calculations, such as multi-phase chemical equilibrium, it is important to synchronize the elements among multiple phases, so that each phase contains the same elements with the same ordering. In such cases, simply use the same string in the elements field for all phases.
Defining the Species¶
The species in the phase are declared in the species field. They are not defined there, only declared. Species definitions may be imported from other files, or species may be defined locally using species entries elsewhere in the file.
If a single string of species symbols is given, then it is assumed that these are locally defined. For each one, a corresponding species entry must be present somewhere in the file, either preceding or following the phase entry. Note that the string may extend over multiple lines by delimiting it with triple quotes:
species = 'AR SI Si2 SiH SiH2 SiH3 SiH4'
# include all species defined in this file
species = 'all'
# a multi-line species declaration
species = """ H2 H O O2 OH H2O HO2 H2O2 C CH
CH2 CH2(S) CH3 CH4 CO CO2 HCO CH2O CH2OH CH3O
CH3OH C2H C2H2 C2H3 C2H4 C2H5 C2H6 HCCO CH2CO HCCOH
N NH NH2 NH3 NNH NO NO2 N2O HNO CN
HCN H2CN HCNN HCNO HOCN HNCO NCO N2 AR C3H7
C3H8 CH2CHO CH3CHO """
If the species are imported from another file, instead of being defined locally, then the string should begin with the file name (without extension), followed by a colon:
# import selected species from silicon.xml
species = "silicon: SI SI2 SIH SIH2 SIH3 SIH4 SI2H6"
# import all species from silicon.xml
species = "silicon: all"
In this case, the species definitions will be taken from file silicon.xml,
which must exist either in the local directory or somewhere on the Cantera
search path.
It is also possible to import species from several sources, or mix local definitions with imported ones, by specifying a sequence of strings:
species = ["CL2 CL F F2 HF HCL", # defined in this file
"air: O2 N2 NO", # imported from 'air.xml'
"ions: CL- F-"] # imported from 'ions.xml'
Note that the strings must be separated by commas, and enclosed in square brackets or parentheses.
Declaring the Reactions¶
The reactions among the species are declared in the reactions field. Just as
with species, reactions may be defined locally in the file, or may be imported
from one or more other files. All reactions must only involve species that have
been declared for the phase.
Unlike species, reactions do not have a name, but do have an optional ID
field. If the ID field is not assigned a value, then when the reaction entry
is read it will be assigned a four-digit string encoding the reaction number,
beginning with '0001' for the first reaction in the file, and incrementing
by one for each new reaction.
If all reactions defined locally in the input file are to be included in the
phase definition, then assign the reactions field the string 'all':
reactions = 'all'
If, on the other hand, only some of the reactions defined in the file are to be
included, then a range can be specified using the reaction ID fields:
reactions = 'nox-12 to nox-24'
In determining which reactions to include, a lexical comparison of id strings is
performed. This means, for example, that 'nox-8' is greater than
'nox-24'. (If it is rewritten 'nox-08', however, then it would be lexically
less than 'nox-24'.)
Just as described above for species, reactions can be imported from another file, and reactions may be imported from several sources. Examples:
# import all reactions defined in this file
reactions = "all"
# import all reactions defined in rxns.xml
reactions = "rxns: all"
# import reactions 1-14 in rxns.xml
reactions = "rxns: 0001 to 0014"
# import reactions from several sources
reactions = ["all", # all local reactions
"gas: all", # all reactions in gas.xml
"nox: n005 to n008"] # reactions 5 to 8 in nox.xml
The Kinetics Model¶
A kinetics model is a set of equations to use to compute reaction rates. In
most cases, each type of phase has an associated kinetics model that is used by
default, and so the kinetics field does not need to be assigned a value. For
example, the ideal_gas entry has an associated kinetics model called
GasKinetics that implements mass-action kinetics, computes reverse rates
from thermochemistry for reversible reactions, and provides various
pressure-independent and pressure-dependent reaction types. Other models could
be implemented, and this field would then be used to select the desired
model. For now, the kinetics field can be safely ignored.
The Transport Model¶
A transport model is a set of equations used to compute transport
properties. For ideal_gas phases, multiple transport models are
available; the one desired can be selected by assigning a string to this
field. See Transport Models for more details.
The Initial State¶
The phase may be assigned an initial state to which it will be set when the
definition is imported into an application and an object created. This is done
by assigning field initial_state an embedded entry of type state,
described in The state entry.
Most of the attributes defined here are “immutable,” meaning that once the
definition has been imported into an application, they cannot be changed by the
application. For example, it is not possible to change the elements or the
species. The temperature, pressure, and composition, however, are “mutable”—
they can be changed. This is why the field defining the state is called the
initial_state; the object in the application will be initially set to this
state, but it may be changed at any time.
Special Processing Options¶
The options field is used to indicate how certain conditions should be handled when importing the phase definition. The options field may be assigned a string or a sequence of strings from the table below.
| Option String | Meaning |
|---|---|
'skip_undeclared_elements' |
When importing species, skip any containing undeclared elements, rather than flagging them as an error. |
'skip_undeclared_species' |
When importing reactions, skip any containing undeclared species, rather than flagging them as an error. |
'skip_undeclared_third_bodies' |
When importing reactions with third body efficiencies, ignore any efficiencies for undeclared species, rather than flagging them as an error. |
'allow_discontinuous_thermo' |
Disable the automatic adjustment of NASA polynomials to eliminate discontinuities in enthalpy and entropy at the midpoint temperature. |
Using the options field, it is possible to extract a sub-mechanism from a large
reaction mechanism, as follows:
ideal_gas(name = 'hydrogen_mech',
elements = 'H O',
species = 'gri30:all',
reactions = 'gri30:all',
options = ('skip_undeclared_elements',
'skip_undeclared_species',
'skip_undeclared_third_bodies'))
If we import this into Matlab, for example, we get a gas mixture containing the 8 species (out of 53 total) that contain only H and O:
>> gas = Solution('gas.cti', 'hydrogen_mech')
hydrogen_mech:
temperature 0.001 K
pressure 0.00412448 Pa
density 0.001 kg/m^3
mean mol. weight 2.01588 amu
1 kg 1 kmol
----------- ------------
enthalpy -3.786e+006 -7.632e+006 J
internal energy -3.786e+006 -7.632e+006 J
entropy 6210.88 1.252e+004 J/K
Gibbs function -3.786e+006 -7.632e+006 J
heat capacity c_p 9669.19 1.949e+004 J/K
heat capacity c_v 5544.7 1.118e+004 J/K
X Y Chem. Pot. / RT
------------- ------------ ------------
H2 1 1 -917934
[ +7 minor] 0 0
>> eqs = reactionEqn(gas)
eqs =
'2 O + M <=> O2 + M'
'O + H + M <=> OH + M'
'O + H2 <=> H + OH'
'O + HO2 <=> OH + O2'
'O + H2O2 <=> OH + HO2'
'H + O2 + M <=> HO2 + M'
'H + 2 O2 <=> HO2 + O2'
'H + O2 + H2O <=> HO2 + H2O'
'H + O2 <=> O + OH'
'2 H + M <=> H2 + M'
'2 H + H2 <=> 2 H2'
'2 H + H2O <=> H2 + H2O'
'H + OH + M <=> H2O + M'
'H + HO2 <=> O + H2O'
'H + HO2 <=> O2 + H2'
'H + HO2 <=> 2 OH'
'H + H2O2 <=> HO2 + H2'
'H + H2O2 <=> OH + H2O'
'OH + H2 <=> H + H2O'
'2 OH (+ M) <=> H2O2 (+ M)'
'2 OH <=> O + H2O'
'OH + HO2 <=> O2 + H2O'
'OH + H2O2 <=> HO2 + H2O'
'OH + H2O2 <=> HO2 + H2O'
'2 HO2 <=> O2 + H2O2'
'2 HO2 <=> O2 + H2O2'
'OH + HO2 <=> O2 + H2O'
Ideal Gas Mixtures¶
Now we turn to the specific entry types for phases, beginning with
ideal_gas.
Many combustion and CVD simulations make use of reacting ideal gas
mixtures. These can be defined using the ideal_gas entry. The Cantera
ideal gas model allows any number of species, and any number of reactions among
them. It supports all of the options in the widely-used model described by Kee
et al. [1], plus some additional options for species thermodynamic
properties and reaction rate expressions.
An example of an ideal_gas entry is shown below:
ideal_gas(name='air8',
elements='N O Ar',
species='gri30: N2 O2 N O NO NO2 N2O AR',
reactions='all',
transport='Mix',
initial_state=state(temperature=500.0,
pressure=(1.0, 'atm'),
mole_fractions='N2:0.78, O2:0.21, AR:0.01'))
This entry defines an ideal gas mixture that contains 8 species, the definitions
of which are imported from dataset gri30 (file gri30.xml). All reactions
defined in the file are to be included, transport properties are to be computed
using mixture rules, and the state of the gas is to be set initially to 500 K, 1
atm, and a composition that corresponds to air.
Transport Models¶
Two transport models are available for use with ideal gas mixtures. The first is
a multicomponent transport model that is based on the model described by
Dixon-Lewis [2] (see also Kee et al. [3]). The second is a model that uses
mixture rules. To select the multicomponent model, set the transport field to
the string 'Multi', and to select the mixture-averaged model, set it to the
string 'Mix':
ideal_gas(name="gas1",
# ...
transport="Multi", # use multicomponent formulation
# ...
)
ideal_gas(name="gas2",
# ...
transport="Mix", # use mixture-averaged formulation
# ...
)
Stoichiometric Solid¶
A stoichiometric_solid is one that is modeled as having a precise,
fixed composition, given by the composition of the one species present. A
stoichiometric solid can be used to define a condensed phase that can
participate in heterogeneous reactions. (Of course, there cannot be homogeneous
reactions, since the composition is fixed.)
stoichiometric_solid(name='graphite',
elements='C',
species='C(gr)',
density=(2.2, 'g/cm3'),
initial_state=state(temperature=300.0,
pressure=(1.0, 'atm')))
In the example above, the definition of the species 'C(gr)' must appear
elsewhere in the input file.
Stoichiometric Liquid¶
A stoichiometric liquid differs from a stoichiometric solid in only one respect: the transport manager computes the viscosity as well as the thermal conductivity.
Interfaces¶
Now that we have seen how to define bulk, three-dimensional phases, we can describe the procedure to define an interface between phases.
Cantera presently implements a simple model for an interface that treats it as a two-dimensional ideal solution of interfacial species. There is a fixed site density \(n^0\), and each site may be occupied by one of several adsorbates, or may be empty. The chemical potential of each species is computed using the expression for an ideal solution:
where \(\theta_k\) is the coverage of species \(k\) on the surface. The coverage is related to the surface concentration \(C_k\) by
where \(n_k\) is the number of sites covered or blocked by species \(k\).
The entry type for this interface model is
ideal_interface. (Additional interface models may be added to allow
non-ideal, coverage-dependent properties.)
Defining an interface is much like defining a phase. There are two new fields:
phases and site_density. The phases field specifies the bulk phases that
participate in the heterogeneous reactions. Although in most cases this string
will list one or two phases, no limit is placed on the number. This is
particularly useful in some electrochemical problems, where reactions take place
near the triple-phase boundary where a gas, an electrolyte, and a metal all meet.
The site_density field is the number of adsorption sites per unit area.
Another new aspect is in the embedded state entry in the
initial_state field. When specifying the initial state of an interface, the
state entry has a field coverages, which can be assigned a string
specifying the initial surface species coverages:
ideal_interface(name='silicon_surface',
elements='Si H',
species='s* s-SiH3 s-H',
reactions='all',
phases='gas bulk-Si',
site_density=(1.0e15, 'molec/cm2'),
initial_state=state(temperature=1200.0,
coverages='s-H:1'))
The state entry¶
The initial state of either a phase or an interface may be set using an embedded
state entry. Note that only one of (pressure, density) may be
specified, and only one of (mole_fractions, mass_fractions, coverages).
References
| [1] | R. J. Kee, F. M. Rupley, and J. A. Miller. Chemkin-II: A Fortran chemical kinetics package for the analysis of gasphase chemical kinetics. Technical Report SAND89-8009, Sandia National Laboratories, 1989. |
| [2] | G. Dixon-Lewis. Flame structure and flame reaction kinetics, II: Transport phenomena in multicomponent systems. Proc. Roy. Soc. A, 307:111–135, 1968. |
| [3] | R. J. Kee, M. E. Coltrin, and P. Glarborg. Chemically Reacting Flow: Theory and Practice. John Wiley and Sons, 2003. |

